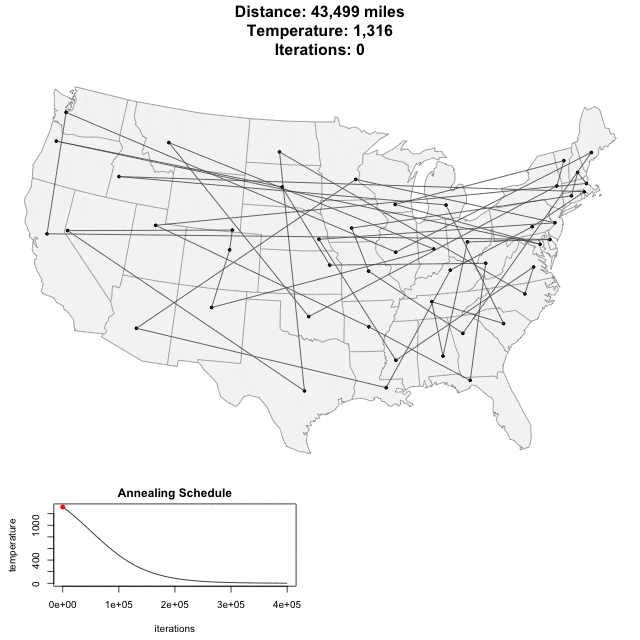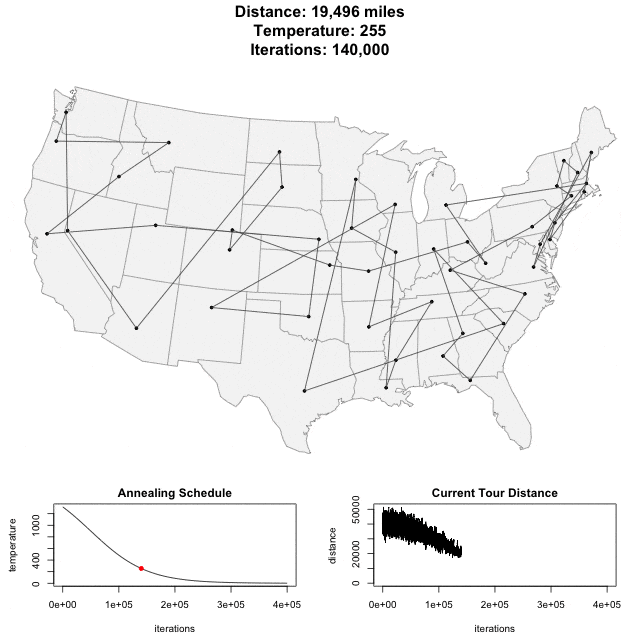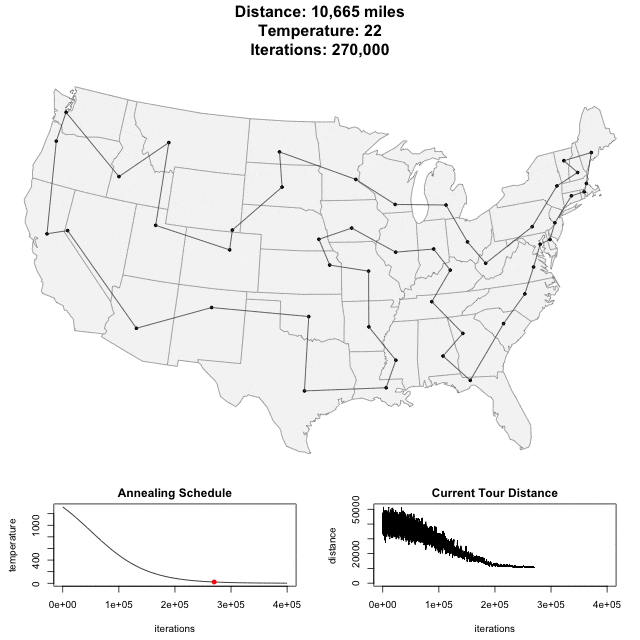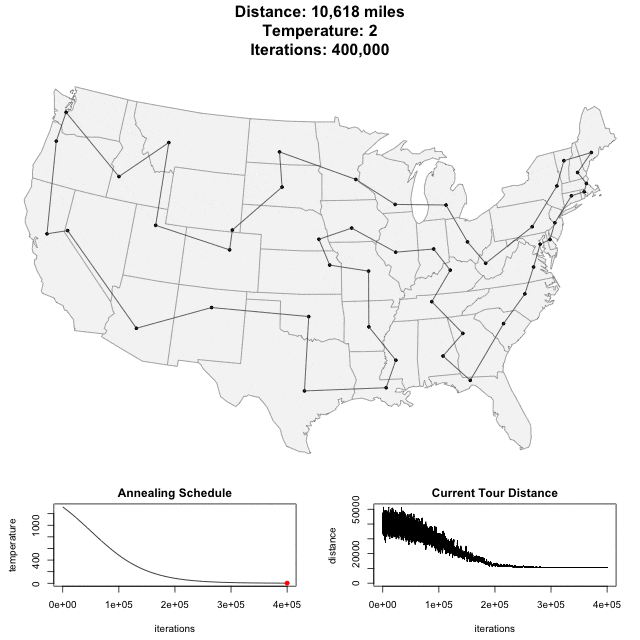
I was introduced to simulated annealing as an optimization algorithm when studying methods useful in integrated circuit design. By adding progressively decreasing noise into the optimization one can break free of local minima. Best results are achieved when the decrease is scheduled to reach zero at the wall clock time allocated to optimization. wikipedia ![]()
To get a feel for the algorithm's behavior I wrote an optimizer in a few lines of Smalltalk with mouse clicks to set up destinations and the optimizer drawing routes as it found them. I sampled the cursor location to control the strength of noise introduced into route length comparisons.
switched.length < current.length + noise ifTrue: [current ← switched]
My algorithm ran fast enough to successfully optimize a few dozen destinations in a few seconds. I could repeat experiments by just waving the cursor back up to scramble the solution and then bring it back down faster or slower while watching the route "organize" on the screen in front of me.
With a quick move I could "freeze" disorder in the route. With a slow move I could repeatedly find the same best route. I could imagine shaking a box of irregular shapes to jumble them or jiggling the box gently coax them into order. I intuitively knew just how to move the cursor to get good results quickly.
I've read, but not proven myself, that an exponential decrease makes the best use of time allocated to the optimization. That is absolutely consistent with my experience.
.
Here’s an animation of the annealing process finding the shortest path through the 48 state capitals of the contiguous United States by Todd Schneider. post ![]()