does involve a starting number
We are about to explore the conceptual foundations of natural numbers in order to understand that numbers are cognitive constructions, and decidedly not part of the natural world.
Kronecker made his famous quote “God made the integers, all else is the work of man.” at a meeting in 1886 (from his obituary, 1823-1891, in Mathematische Annalen 43:1-25). It was recently publicized as the title of a book by Stephen Hawking, God Created the Integers: The mathematical breakthroughs that changed history (2007). The quote is associated with Kronecker’s belief that mathematics should address finite numbers and should avoid the irrational numbers, a position similar to that taken here with regard to real numbers. But there is no need to interject metaphysics, man created the rationals as well as the irrationals. Brian Smith (On the Origin of Objects, 1996, p.355) comments that Kronecker got it backwards. Metaphysics arises out of indefiniteness, the absence of boundaries, from which we then carve out the discrete numbers. Irving Stein (The Concept of Object as the Foundation of Physics, 1996, abstract) points to the first distinction: “Objects arise from restrictions on nonspace.”
Fields medalist Michael Atiyah draws the analogy of a jellyfish living in an ocean that provides perceptual continuity but not discrete objects. From an online interview 12/2016 at webofstories ![]()
> We see individual objects and if the universe were different and we didn’t have individual objects around us we just had a Sea, a mass of continuity...counting would not be natural.
The systems viewpoint is that the web of interrelations between things is closer to reality than the things we create via perceptual discrimination.
~
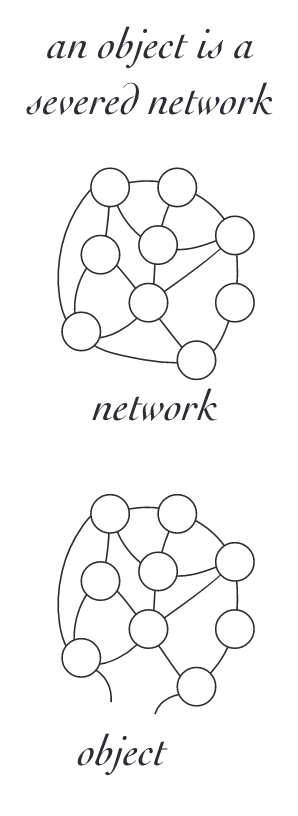
An object is a severed network
In reality, everything is intricately woven into **one unified Whole**. Reality is not fragmented, nor is it indexed, nor is it linear, nor is it enumerated. It is human cognition that first constructs objects and then abstracts them sufficiently to be able to determine how many. What we perceive as objects are differences that we impose, boundaries that we construct in support of our own unique perspectives. We construct an object by severing it from a woven context.
Very few things actually meet the criterion of being countable. Figure 9-1 provides a listing of some of the things we can and cannot count. Foremost is the idea that we ignore sufficient detail to be able to put things into the same category so that one of them and one of them makes two of the same them. Even the word object is misleading, since it presumes that we have already forgotten sufficient detail to be able to detach our personal definition of thing from the web of interrelations to see it as a discrete thing.[7] We have drawn a distinction around selected relations.
[7] These distinctions are important because the epistemology that generates counting is no longer adequate for understanding and acting responsibly in the world. Our world is a complex network of interrelations. Physical objects do not have an independent existence, we carve them out of the web of reality by making cognitive distinctions.
We will not be able to reach a necessary holistic perspective on our Earth, we will not have access to ecological thinking with our current object-oriented perception of how to count what counts. Quantum mechanics leads the way to understanding the essential indeterminism of objects. Non-linear dynamics reinforces the idea that reality is a network of interdependencies. We look at a forest and see individual trees, unable to comprehend that 2/3 of each tree is below ground. It is the dense interweaving of roots that is the forest’s cognitive network. In essence, counting destroys the richness of reality.
Objects are defined by their interactions rather than by their independent properties. Put colorfully, a hand is not five fingers, it is thirty-two relations between fingers. The uncountable constructions of our minds illustrate clearly the limitations of arithmetic. We cannot count thoughts, feelings, beliefs, the wind, a river, sunshine, frost, the internet, a conversation or the web of life. We can count peaks but not mountains, snowflakes but not snow, branches but not roots, heartbeats but not metabolism, airplanes but not clouds, notes but not music, words but not ideas. We cannot count things that change faster than our ability to assign numbers to them. We cannot count the discrete packets of data distributed over the internet because there are too many and they change too quickly. If we were to freeze the internet, or any physiological process, or any natural process, we might be able to count the static pieces that break off but we would be counting only the fragments of a dead thing, the living thing would have moved on to be something different. We cannot accurately say out loud the national debt (even if we could count the dollars) because by the time it was out of our mouths, the debt would have changed by a personal fortune.
There is no 3 in our physical reality, only 3-of.[8] Every object/interrelation within the physical world is unique and entangled. Uniqueness is a consequence of participation in a contextual web of interrelations. Counting then is a process of successively making and dissolving distinctions, with the goal of removing all uniqueness and discernibility from an interaction with physical reality.
[8] For example, every rabbit is unique. When we see a rabbit on the lawn, our perceptional system constructs an experiential replica. Facets of that replica fit categories we have established from prior experience. We have in mind one replica of our personal category rabbit. Now we might look closer and see three rabbits. The cardinality of that ensemble can be assigned a number, the number of rabbits. However, if we introduce a different (imposed) perceptual category, say age, we cease to have three rabbits and may have instead one parent and two children. Cardinality depends upon not only a cognitive category but also the ability to hold that category consistent in a dynamically changing perceptual environment.
Similarly, addition does not apply to abstract numbers. Only 2-of and 3-of can be added together. This viewpoint is virtually opposite to the idea that mathematical operations are independent of application. The sum of the concept 2 and the concept 3 is a symbolic definition, not an operation in the sense of put together. Technically, the set of two {o1,o2} put together with the set of three {o3,o4,o5} is a new set with two members, {{o1,o2},{o3,o4,o5}}. In order to get to five, the two sets need to be joined by Union; addition over sets, not addition over elements. To apply the Union operation, members need to be indexed so that they can be uniquely identified, since Union does not support duplicates. Addition as fusion avoids these issues.
In his development of semiotics, C. S. Peirce identified three types of abstract reference. An icon indicates by looking like what it represents. Delimiting brackets are an iconic representation of containers. An index tallies, it is connected to what it represents, it draws attention but does not resemble. While being constructed, tally marks are indices. A sign is arbitrary, with no connection to what it represents other than convention. Words are signs.
Conventional counting (1, 2, 3,...) does not count objects, it is rather an indexing scheme. Richard Heck: “Counting... has nothing essential to do with equinumerosity (let alone one-to-one correspondence).”9 Conventionally we assign an index to each object by adding 1 to the index of the prior object. We do not add 1 to the object itself, we add it to the running tally. Any difference will do for indexing, numbers are only a convenience. The running sequence too has nothing to do with a tally, it is yet another cognitive scheme to keep track of thoughts. We do not assign n + 1 to a particular object, any one that remains unindexed will do.
The distinction between object and indicator is the Fundamental Principle of General Semantics.10
**General Semantics** *Do not confuse the thing itself with the tally mark that we have associated with it.*
The indistinguishability of tallies is essential to our ability to count them, otherwise the differences between them would overshadow the similarity that underlies their ensemble.
For the collection of furniture, we can assign the number 1 to the table, or to any of the chairs, or to any of the items. Similarly for 2, 3, etc. Clearly there is no preferential “Item 3”. The item that receives the number 3 can change if we were to count again, even though the total number of items does not change. Figure 9-2 provides a visual example. If you have ever watched a toddler learning to count, you will see the profound confusion caused by our arbitrary assignment of sequential numbers to objects.11
[…]
Figure 9-3: The choreography of counting
~
Bricken, Iconic Arithmetic Volume I.
COUVALIS, George, 2013. Philoponus’s Traversal Argument and the Beginning of Time. Modern Greek Studies (Australia and New Zealand). 2013. No. Special Issue, p. 68–78.