[…] a new kind of symbol called a Point, which may be thought of as a group of dots. To be an abbreviated formula the series of symbols must satisfy the conditions:
(a) The brackets must be properly paired, i.e., if we go on removing pairs of brackets which face each other and have no other brackets between them there should eventually be no brackets left. The brackets appearing in an abbreviated formula will often be described as 'explicitly shown brackets.'
(b) Of a pair of brackets one must occur adjacent to an operator and one not. The expression 'adjacent to an operator' is used here and elsewhere to mean 'adjacent to a dyadic operator or adjacent to and on the right of a monadic operator.'
(c) If inthe formula we replacedyadic operatorsby 'D', monadicoperators by 'Ml', irreducibleformulaeby 'x' and points by ':', calling the resultthe 'projectedformula,'then the firstsymbolof a projectedabbreviatedformula mustbe '(', 'x', or 'M' and thelast, ')' or 'x'. A pair ofconsecutivesymbolsin the projectedformulamust be 'x)', '(x', '))', 'M(', 'D(', ')D', '(M' or '((' or else part of one of the followingseriesofthree: 'x:D', 'D:x', 'M:x', '):D', 'D:(', 'l:(', 'D:M', 'M:M': in the lattercase the wholeseriesofthreesymbolsmust be part of the projected formula.
We wantoneand onlyoneformulato correspondto each abbreviatedformula. Such a correspondenci es definedbelow in termsof an orderingof the points. I shallfollowRussell's terminolog a ynd speak ofthe earlierof twopointsin the orderingas being of higherpowerthan the other. Curryuses the expression 'seniorto' and Quine,whosepointsare called 'joints,'uses 'looserthan.' The powerof a point may depend on any formalrelationshipsbetweenthe point and the formulait occursin, and varies fromsystemto system.
[…]
The scopes of two pointscan neverbe strictlyoverlapping. Suppose that thescopeofone pointis limitedby bracketsa and a ofwhicha is the one further to the left, and the otherby and a of whichyis to theleft; alsothat a is tothe left of , and that the scopesstrictlyoverlap,so thatthe bracketsforma figure like this:
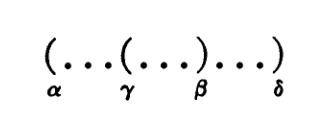
Uploaded image
The pointsfromwhichthesebracketsarisecan be eitherat a and y,or ata and 3,or at, and y,or at ,and S. The considerationofthelast alternativecan be omittedas it isthe sameas the firstapart frominterchangeof leftand right.
[…]
~
TURING, A. M., 1942. The use of dots as brackets in Church’s system. Journal of Symbolic Logic. December 1942. Vol. 7, no. 4, p. 146–156. DOI 10.2307/2268111. [Accessed 10 December 2023].