To keep things tolerably simple, Stephen Wolfram is not going to talk directly about rules that operate on hypergraphs.
> Instead Iʼm going to talk about rules that operate on strings of characters. (To clarify: these are not the strings of string theory—although in a bizarre twist of “pun‐becomes-science” I suspect that the continuum limit of the operations I discuss on character strings is actually related to string theory in the modern physics sense.)
OK, so letʼs say we have the rule:
{A → BBB, BB → A}
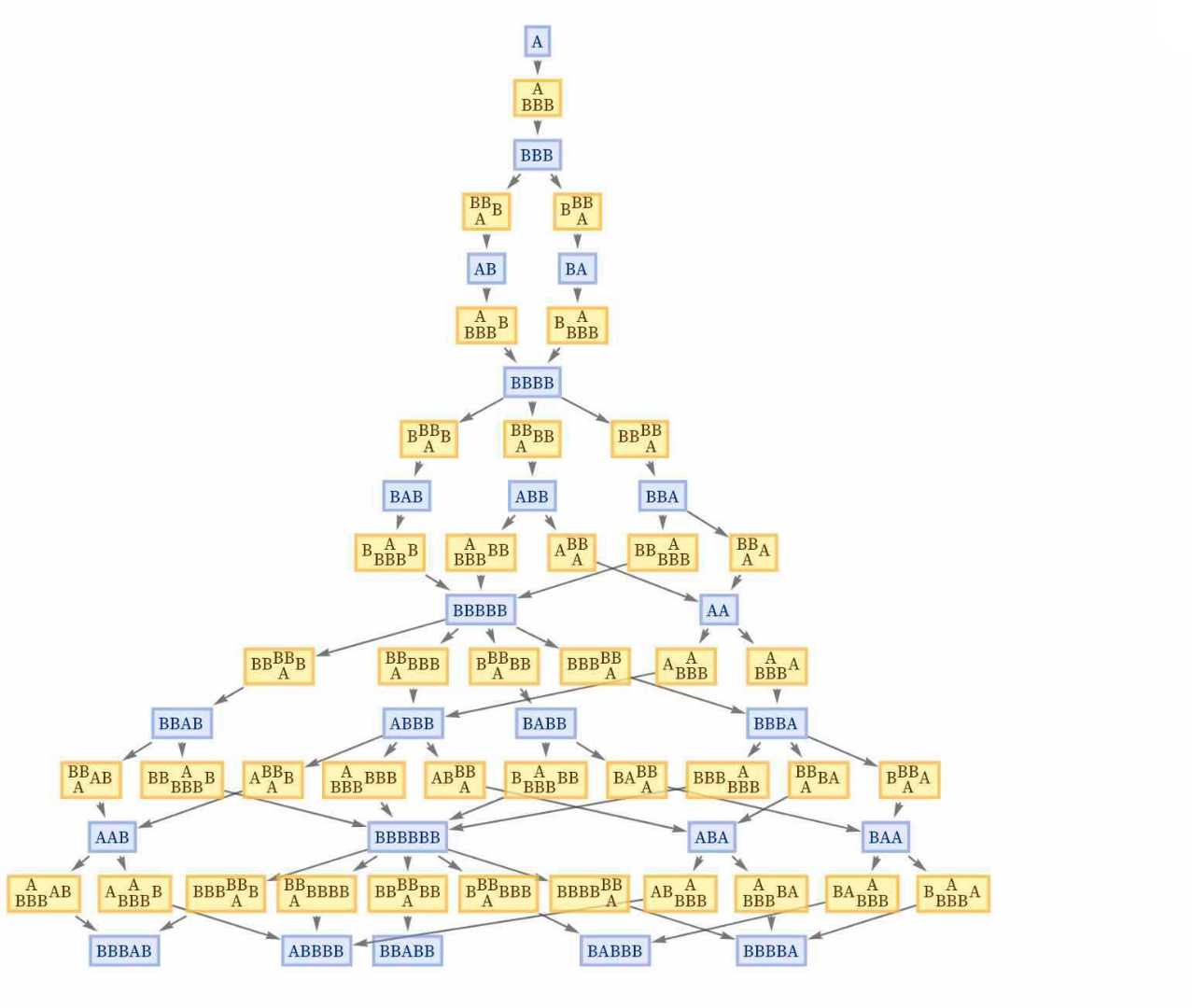
This rule says that anywhere we see an A, we can replace it with BBB, and anywhere we see BB we can replace it with A. So now we can generate what we call the Multiway System for this rule, and draw a “Multiway Graph” that shows everything that can happen: […]
At the first step, the only possibility is to use A→BBB to replace the A with BBB. But then there are two Possibilities: replace either the first BB or the second BB—and these choices give different results. On the next step, though, all that can be done is to replace the A—in both cases giving BBBB.
So in other words, even though we in a sense had two paths of history that diverged in the multiway system, it took only one step for them to converge again. And if you trace through the picture above youʼll find out thatʼs what always happens with this rule: every pair of branches that is produced always merges, in this case after just one more step.
This kind of balance between branching and merging is a phenomenon Stephen Wolfram calls “Causal Invariance”. And while it might seem like a detail here, it actually turns out that itʼs at the core of why relativity works, why thereʼs a meIaningful objective reality in quantum mechanics, and a host of other core features of fundamental physics.
But letʼs explain why he calls the property causal invariance. The picture above just shows what “state” (i.e. what string) leads to what other one. But at the risk of making the picture more complicated (and note that this is incredibly simple compared to the full hypergraph case), we can annotate the multiway graph by including the updating Events that lead to each transition between states:
Annotate the multiway graph
But now we can ask the question: what are the causal relationships between these events? In other words, what event needs to happen before some other event can happen? Or, said another way, what events must have happened in order to create the input thatʼs needed for some other event?
Let us go even further, and annotate the graph above by showing all the causal dependencies between events: […]
The orange lines in effect show which event has to happen before which other event—or what all the causal relationships in the multiway system are. And, yes, itʼs complicated. But note that this picture shows the whole multiway system—with all possible paths of history as well as the whole network of causal relationships within and between these paths.
But hereʼs the crucial thing about causal invariance: it implies that actually the graph of causal relationships is the same regardless of which path of history is followed. And thatʼs why Stephen Wolfram originally called this property “causal invariance”—because it says that with a rule like this, the causal properties are invariant with respect to different choices of the sequence in which updating is done.
And if one traced through the picture above (and went quite a few more steps), one would find that for every path of history, the causal graph representing causal relationships between events would always be: […]
or, drawn differently, […]
~
WOLFRAM, Stephen, 2020. A project to find the fundamental theory of physics. . Champaign, IL: Wolfram Media, Inc. ISBN 978-1-57955-035-6.