As an example where logistic functions are usually assumed to be very steep and are thus often replaced by a step function (and vice versa) we can point out the perceptrons considered in artificial neural networks (Fig. 2).
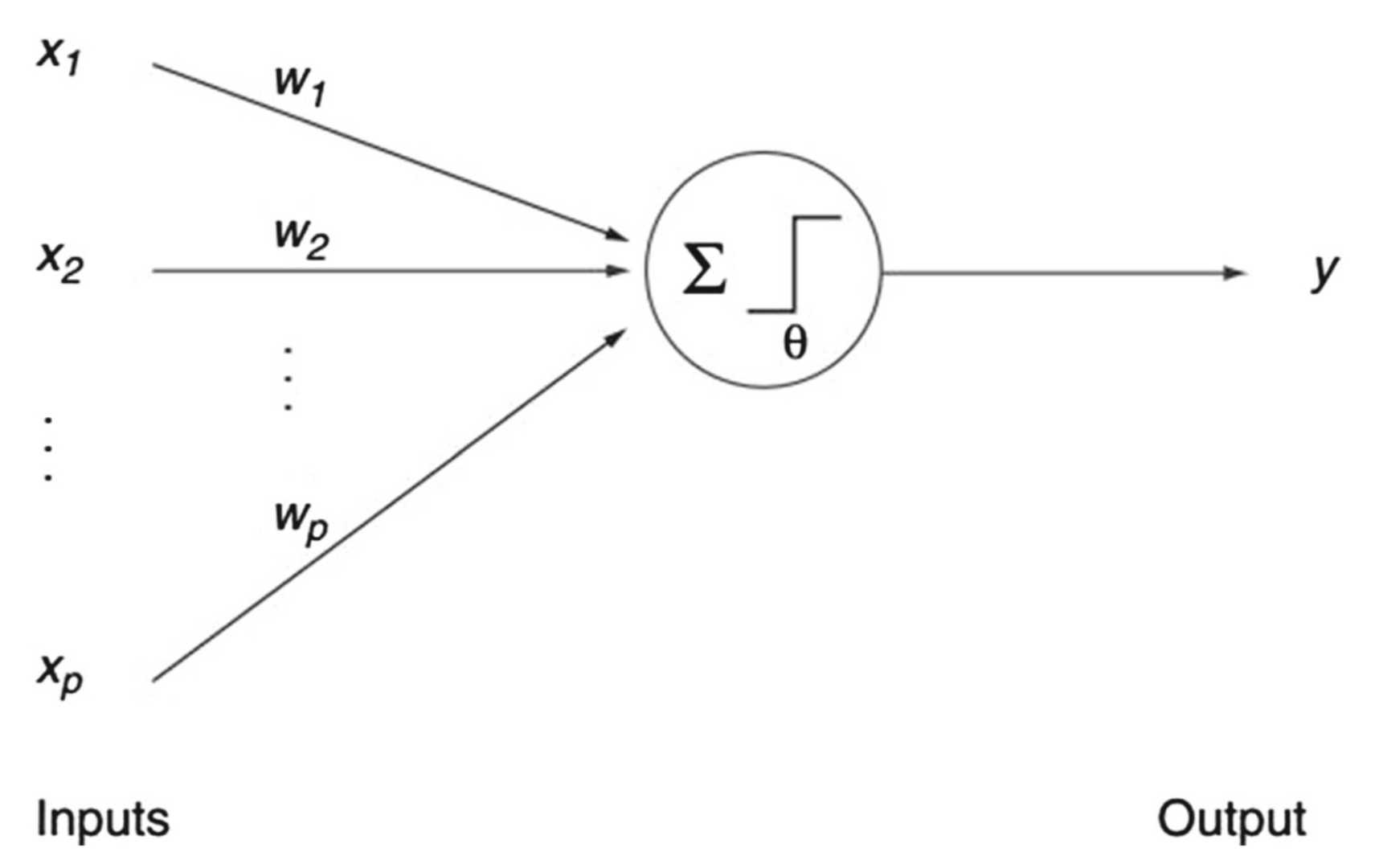
Fig. 2 The perceptron of Rosenblatt
F. Rosenblat, The perceptron: a probabilistic model for information storage and organization in the brain, Cornell aeronautical laboratory. Psychol. Rev. 65, 386–408 (1958)
KYURKCHIEV, Nikolay and MARKOV, Svetoslav, 2016. On the Hausdorff distance between the Heaviside step function and Verhulst logistic function. Journal of Mathematical Chemistry. Online. 1 January 2016. Vol. 54, no. 1, p. 109–119. [Accessed 27 February 2023]. DOI 10.1007/s10910-015-0552-0. In this note we prove more precise estimates for the approximation of the step function by sigmoidal logistic functions. Numerical examples, illustrating our results are given, too.
In this work we study the behavior of the family of logistic functions whenever their slope increases. From (bio-)chemical point of view we may wish to know when an autocatalytic reaction with rate k can be assumed as instantaneous. In practice, we may assume that the reaction is instantaneous if its rate is such that the corresponding H-distance (between the logistic and the step function) is less than the precision of the measurement instruments used in the experiment. To achieve our goal we obtain new sharper estimates for the H-distance between a step function and its best approximating logistic function.