In the mathematical study of Cellular Automata, Rule 90 is an elementary cellular automaton based on the exclusive or function. wikipedia ![]()
It consists of a one-dimensional array of cells, each of which can hold either a 0 or a 1 value. In each time step all values are simultaneously replaced by the exclusive or of their two neighboring values. wikipedia ![]()
Martin, Odlyzko & Wolfram (1984) call it "the simplest non-trivial cellular automaton", and it is described extensively in Stephen Wolfram's 2002 book A New Kind of Science.
WOLFRAM, Stephen, 1983. Statistical mechanics of cellular automata. Reviews of Modern Physics. 1 July 1983. Vol. 55, no. 3, p. 601–644. DOI 10.1103/RevModPhys.55.601. Cellular Automata are used as simple mathematical models to investigate self-organization in statistical mechanics. A detailed analysis is given of “elementary” cellular automata consisting of a sequence of sites with values 0 or 1 on a line, with each site evolving deterministically in discrete time steps according to definite rules involving the values of its nearest neighbors. With simple initial configurations, the cellular automata either tend to homogeneous states, or generate self-similar patterns with fractal dimensions ≃ 1.59 or ≃ 1.69. With “random” initial configurations, the irreversible character of the cellular automaton evolution leads to several self-organization phenomena. Statistical properties of the structures generated are found to lie in two universality classes, independent of the details of the initial state or the cellular automaton rules. More complicated cellular automata are briefly considered, and connections with dynamical systems theory and the formal theory of computation are discussed.
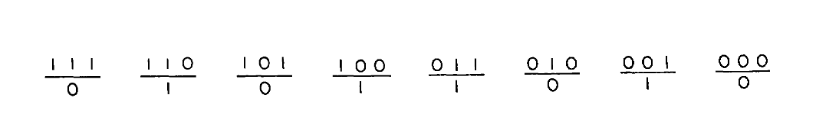
FIG. 1. Example of a set of local rules for the time evolution of a one-dimensional elementary cellular automaton. (Wolfram, Statistical mechanics of cellular automata, p. 604)
// Define the rules const rules = { "000": "0", "001": "1", "010": "0", "011": "1", "100": "1", "101": "0", "110": "1", "111": "0", };
The variables at each site may take values 0 or 1. The eight possible states of three adjacent sites are given on the upper line. The lower line then specifies a rule for the time evolution of the cellular automaton by giving the value to be taken by the central site of the three on the next time step. The time evolution of the complete cellular automaton is obtained by simultaneous application of these rules at each site for each time step.
The rule given is the modulo-two rule: the value of a site at a particular time step is simply the sum modulo two of the values of its two neighbors at the previous time step. Any possible sequence of eight binary digits specifies a cellular automaton.
// Create an initial state let state = "01011010";
// Apply the rules to generate the next state function next(state) { let next = ""; for (let i = 0; i < state.length - 2; i++) { let pattern = state.slice(i, i + 3); next += rules[pattern]; } return next; }
// Create a canvas and draw the states const canvas = document.getElementById("canvas"); const ctx = canvas.getContext("2d"); ctx.fillStyle = "black"; ctx.fillRect(0, 0, canvas.width, canvas.height); ctx.fillStyle = "white"; ctx.font = "16px monospace"; for (let i = 0; i < 100; i++) { ctx.fillText(state, 10, (i + 1) * 20); state = next(state); }
//wiki.ralfbarkow.ch/assets/pages/snippet-template/esm.html
We modified the esm.html file to include a <canvas> element in the body section. See "Basic usage of canvas" mdn ![]() .
.