This is like having a small Child, who has a limited language.
There are things which we cannot explain to him in his own language — not only because his vocabulary is too small, for it would be possible to define new words to him but because he is short of structure, that is syntax, too. We try to convince him that something should or should not be done. Why? he asks; and why? again when we have answered him once. We struggle in his language with these questions. The process may prove impossible, just because the language is inadequate. When we conclude: ‘Because I say so’, we have made a metalinguistic statement. (Incidentally, was it true to say that we could define new words through the existing language? And if not, if for instance we need to demonstrate things as part of the definition, shall we not have swallowed the original language in a metalanguage by so doing? Thinking about such questions is helpful in mastering the new concepts.)
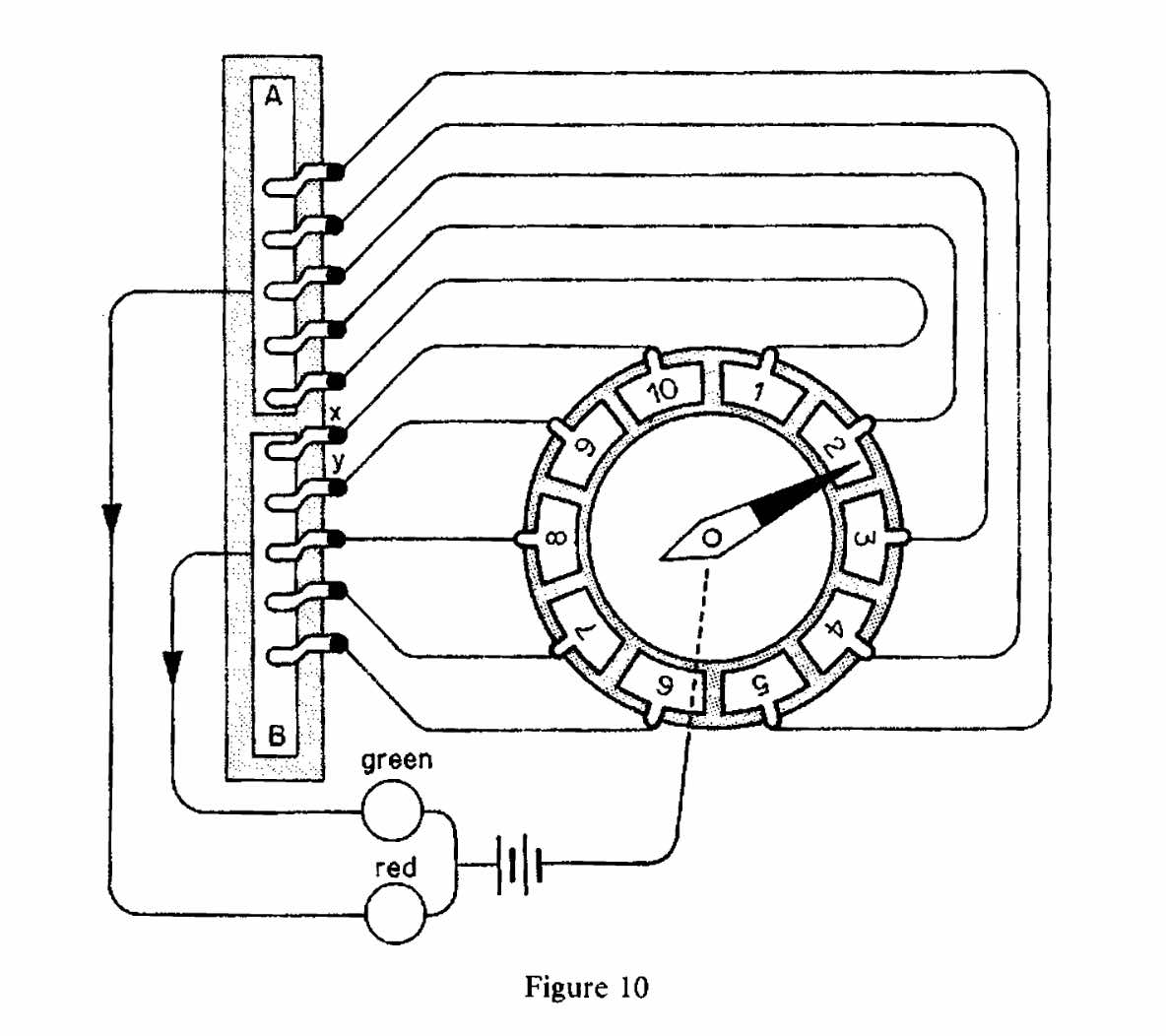
Figure 10
With this preamble, let us now invent a simple machine for doing heuristics. The sensorium consists of a strip of wood, on which are mounted two brass strips A and B. Figure 10 shows that they are insulated from each other.
The afferent part of this machine consists of ten fixed terminals (the dots) bearing spring clips which make electrical connections with the brass strips — five on each. Input arrives down one of the ten wires leading from the roulette wheel, which represents the outside world. The wheel is spun, and the afferent system recognizes that the world outside has taken on one of the values 1 to 10. The efferent part of the machine now goes into action. It has two effectors: the wires leading from A and B to two lights, red and green. One of these bulbs must light up, but there is no way of knowing which. If we go on spinning the wheel it is obvious that, on average, each will light up on half the occasions.
The description just given is written in machine language. All the statements are verifiable in terms of the machine itself. We may use this language, for instance, to declare that red has a 50 per cent chance and green has a 50 per cent chance. The maching itself could ‘understand’ such a statement, because it is derived from its own structure. But there is no way of stating in this language that red is in any sense preferable to green or vice versa. As far as the machine is concerned, such a statement is neither true nor false. It is not verifiable or testable. It is strictly meaningless. In machine language it cannot be said.
Along comes a speaker of metalanguage one — call it Meta 1. This is a language designed to talk about colours and the emotions which colours evoke. He says: ‘I like red, but I don’t like green.” He cannot interfere with nature, which is spinning the wheel. He reckons he wants to train the machine to go red, and this is just like training a dog to respond to a command. He cannot explain in machine language, and the machine does not understand his language. So he communicates with the machine through an ⇒ Algedonic Loop. Here is another new term which must be explained.
[…]
In our invention, it follows, we must provide the machine with an algedonic receptor, through which the speaker of Meta 1 can communicate. This consists of two switches, either of which will move the wooden strip vertically up or down the diagram. The strip in Figure 10 carries and now moves the brass plates A and B; but the contacts from the roulette wheel do not move. The red light, which our observer likes, is activated by the brass strip A. To reward the machine for shining red, we shall tell him, one presses the switch marked Reward. This will move the strip down a notch, and bring the contact marked X on to strip A, whereas it used to rest on B. (Remember that the contacts are fixed). This alters the 50-50 probability of the outcome to 60-40 in favour of Red. If the green light comes on nevertheless, as it may, the machine has to be punished. The observer is told to press the switch marked Punish. (Both switches in fact pull the wooden strip one notch down, but no one but ourselves know this.) The contact Y will now rest on strip A as well, and the probability of a red outcome is now 70 per cent. It is readily seen that the algedonic loop will cause the machine to adapt its behaviour to a red outcome, since that is the decision in Meta 1. The machine does not understand why its behaviour is being conditioned, and the operator does not know how the trick is done. We do, because we are omniscient with respect to this situation. If we were not, we might be puzzled too; most people are, as a matter of fact, when they see this machine working.
~
Stafford Beer, Brain of the firm: the managerial cybernetics of organization, 2d ed (Chichester [Eng.] ; New York: J. Wiley, 1981), p. 58–60.