Instead of basing a search method on comparisons between keys, we can make use of their representation as a Sequence of digits or alphabetic characters.
Consider, for example, the thumb index on a large dictionary; from the first letter of a given word, we can immediately locate the pages that contain all words beginning with that letter.
If we pursue the thumb-index idea to one of its logical conclusions, we come up with a searching scheme based on repeated “subscripting” as illustrated in Table 1.
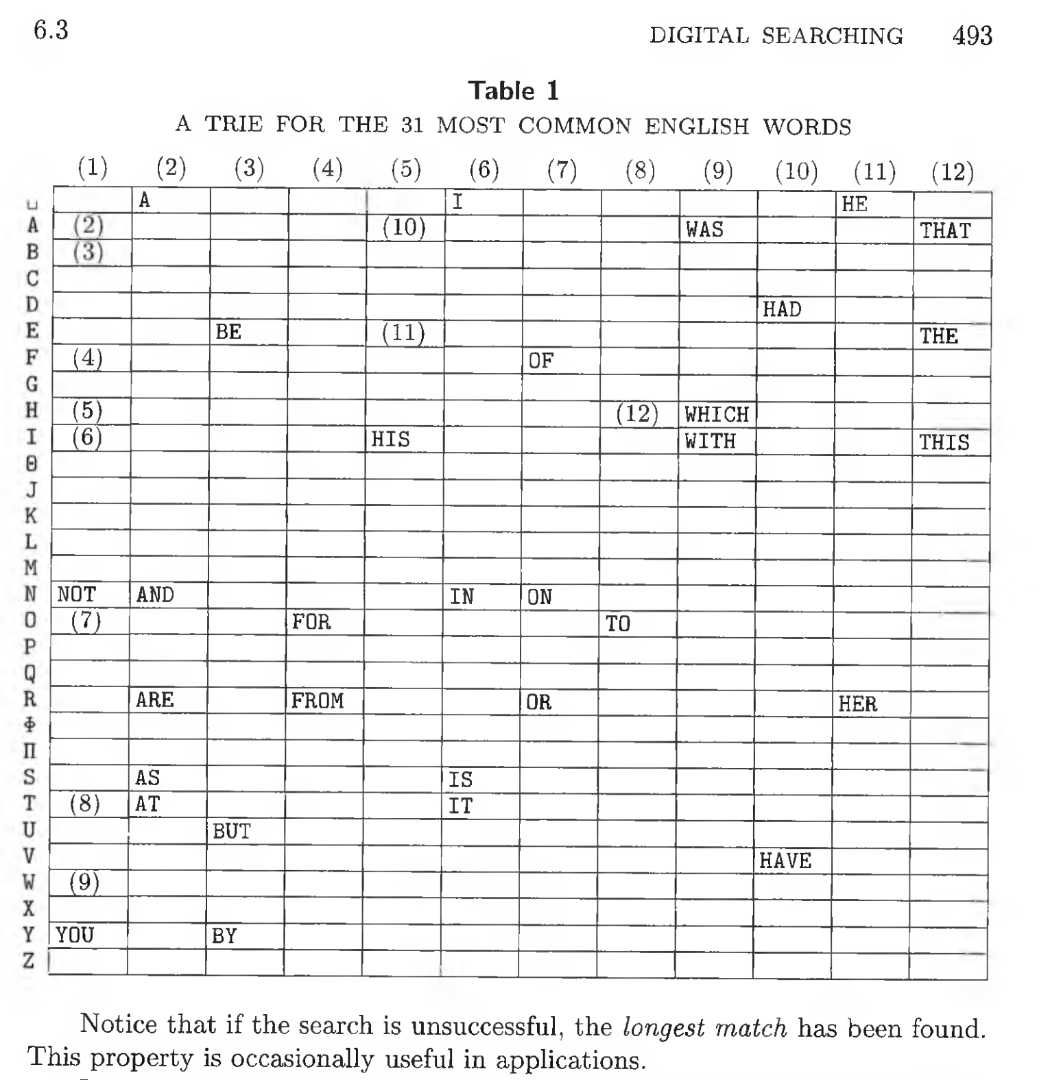
Table 1. A TRIE FOR THE 31 MOST COMMON ENGLISH WORDS
Suppose that we want to test a given search argument to see whether it is one of the 31 most common words of English (see Figs. 12 and 13 in Section 6.2.2). The data is represented in Table 1 as a trie structure; this name was suggested by E. Fredkin [CACM 3 (1960), 490–500] because it is a part of information retrieval.
A Trie — pronounced “try” — is essentially an M-ary tree, whose nodes are M-place vectors with components corresponding to digits or characters. Each node on level l represents the set of all keys that begin with a certain sequence of l characters called its prefix; the node specifies an M-way branch, depending on the (l + 1)st character.
For example, the trie of Table 1 has 12 nodes; node (1) is the root, and we look up the first letter here. If the first letter is, say, N, the table tells us that our word must be NOT (or else it isn’t in the table). On the other hand, if the first letter is W, node (1) tells us to go on to node (9), looking up the second letter in the same way; node (9) says that the second letter should be A, H, or I. The prefix of node (10) is HA. Blank entries in the table stand for null links.
The node vectors in Table 1 are arranged according to MIX character code. This means that a trie search will be quite fast, since we are merely fetching words of an array by using the characters of our keys as subscripts. Techniques for making quick multiway decisions by subscripting have been called “table look-at” as opposed to “table look-up” [see P. M. Sherman, CACM 4 (1961), 172–173, 175].
[…] The nodes of the Trie are vectors whose subscripts run from 0 to M − 1; each component of these vectors is either a key or a link (possibly null).
~
KNUTH, Donald Ervin, 1997. The art of computer programming. v. 3. Sorting and Searching. 2nd ed. Reading, Mass: Addison-Wesley. ISBN 0-201-89685-0, p. 492–493.