KAUFFMAN, L.H., 2001. The mathematics of Charles Sanders Peirce. Cybernetics & Human Knowing. 1 January 2001. Vol. 8, no. 1–2, p. 79–110. pdf 
> This essay explores the Mathematics of Charles Sanders Peirce. We concentrate on his notational approaches to basic logic and his general ideas about Sign, Symbol and diagrammatic thought. In the course of this paper we discuss two notations of Peirce, one of Nicod and one of Spencer-Brown. Needless to say, a notation connotes an entire language and these contexts are elaborated herein. The first Peirce notation is the portmanteau (see below) Sign of illation. The second Peirce notation is the form of implication in the existential graphs (see below). The Nicod notation is a portmanteau of the Sheffer stroke and an (overbar) negation sign. The Spencer-Brown notation is in line with the Peirce Sign of illation. It remained for Spencer-Brown (some fifty years after Peirce and Nicod) to see the relevance of an arithmetic of forms underlying his notation and thus putting the final touch on a development that, from a broad perspective, looks like the world mind doing its best to remember the significant patterns that join logic, speech and mathematics. The movement downward to the Form ('we take the form of distinction for the form.’[9, Chapter 1, page 1]) through the joining together of words into archetypal portmanteau Signs can be no accident in this process of return to the beginning.
# The Logical Garnet The purpose of this section is to point out a remarkable connection between Laws of Form, the Existential Graphs of Peirce, polyhedral geometry, mirror symmetry and the work of Shea Zellweger. (p. 93)
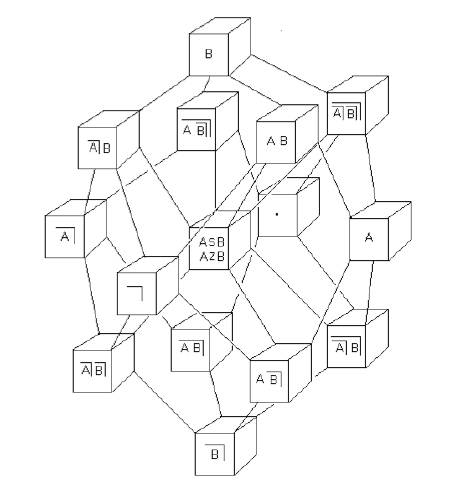
Zellweger did an extensive study of the sixteen binary connectives in Boolean logic ( “and”, “or” and their relatives — all the Boolean functions of two variables), starting from Peirce’s own study of these patterns. He discovered a host of iconic notations for the connectives and a way to map them and their symmetries to the vertices of a four dimensional cube and to a three dimensional projection of that cube in the form of a rhombic dodecahedron. Symmetries of the connectives become, for Zellweger, mirror symmetries in planes perpendicular to the axes of the rhombic dodecahedron. See Figure 2. Zellweger uses his own iconic notations for the connectives to label the rhombic dodecahedron, which he calls the “Logical Garnet”.
This is a remarkable connection of polyhedral geometry with basic logic. The meaning and application of this connection is yet to be fully appreciated. It is a significant linkage of domains. On the one hand, we have logic embedded in everyday speech. One does not expect to find direct connections of the structure of logical speech with the symmetries of Euclidean Geometry. It is the surprise of this connection that appeals to the intuition. Logic and reasoning are properties of language/mind in action. Geometry and symmetry are part of the mindset that would discover eternal forms and grasp the world as a whole. To find, by going to the source of logic, that we build simultaneously a world of reason and a world of geometry incites a vision of the full combination of the temporal and the eternal, a unification of action and contemplation. The relationship of logic and geometry demands a deep investigation. This investigation is in its infancy.
In this section I will exhibit a version of the Logical Garnet (Figure 2) that is labeled so that each label is an explicit function of the two Boolean variables A and B. A list of these functions is given in Figure 1. We will find a new symmetry between the Marked and Unmarked states in this representation. In this new symmetry the mirror is a Looking Glass that has Peirce on one side and Spencer-Brown on the other!
Before embarking on Figure 1, I suggest that the reader look directly at Figure 2. That Figure is a depiction of the Logical Garnet. Note the big dichotomies across the opposite vertices. These are the oppositions between Marked and Unmarked states, the opposition between A and not A, and the opposition between B and not B. If you draw a straight line through any pair of these oppositions and consider the reflection in the plane perpendicular to this straight line, you will see one of the three basic symmetries of the connectives. Along the A/not A axis the labels and their reflections change by a cross around the letter A. Along the B/not B axis, the labels change by a cross around the letter B. These reflections correspond to negating A or B respectively. Along the Marked/Unmarked axis, the symmetry is a bit more subtle. You will note the corresponding formulas differ by a cross around the whole formula and that both variables have been negated (crossed). Each mirror plane performs the corresponding symmetry through reflection. In the very center of the Garnet is a double labeled cube, labeled with the symbols “A S B” and “A Z B”. These stand for “Exclusive Or” and its negation. We shall see why S and Z have a special combined symmetry under these operations. The rest of this section provides the extra details of the discussion.
Let us summarize. View Figure 2. Note that in this three-dimensional figure of the Logical Garnet there are three planes across which one can make a reflection symmetry. Reflection in a horizontal plane has the effect of changing B to its crossed form in all expressions. Reflection in a vertical plane that is transverse to projection plane of the drawing, interchanges A and its crossed form. Finally, reflection in a plane parallel to the projection plane of the drawing interchanges marks with unmarks. We call this the Marked/Unmarked symmetry. (p. 95)
*On first pass, the reader may wish to view Figure 2 directly, think on the theme of the relationship of logic and geometry, and continue into the next section. The reader who wishes to see the precise and simple way that the geometry and logic fit together should read the rest of this section in detail.*
Figure 1 is a list of the sixteen binary connectives given in the notation of Laws of Form. Each entry is a Boolean function of two variables. In the first row we find the two constant functions, one taking both A and B to the marked state, and one taking both A and B to the unmarked state (indicated by a dot). In row two are the functions that ignore either A or B. The remaining rows have the functions that depend upon both A and B. The reader can verify that these are all of the possible Boolean functions of two variables. The somewhat complicated looking functions in the last row are “Exclusive Or” , A S B and its negation A Z B.
[…]
This graphical pattern can be viewed as the lattice of inclusions of these functions regarded as subsets of a universal set. To see this clearly, view the next diagram where we have labeled the vertices of the graph in standard notation with an upward pointing wedge denoting intersection (“and”), a downward pointing wedge denoting union (“or”), 0 denoting empty set and 1 denoting the universe. Then, going outward from 0, pairs of vertices are connected to vertices denoting the union of their labels until we reach the whole universe which is denoted by 1. This lattice is exactly the graph of the rhombic dodecahedron (Diagram 3). (p. 99)
~
LOGICAL GARNET. jpg
http://www.joostrekveld.net/wp/?p=640
Came across this nice interview with Shea Zellweger in Cabinet Magazine, in which he explains why and how he developed his own logical notation. I really liked this part: > “To me it’s important not to just be able to do something, like driving a car. I also want to know how the thing works. In my notation, you could say that the design puts what’s under the hood onto the dashboard, so you learn how the vehicle works while you’re actually driving it. This makes the whole act of driving much less passive, and ultimately much more satisfying. I also like the fact that one’s interaction with my notation is literally hands-on and physical, rather than just all in your head. Knowledge shouldn’t be disconnected from the body. The body should be used as much as possible as a part of the means through which we acquire and store knowledge. Why can’t logic be like that too?”
On his own logic alphabet site there are more explanations of his notation and his intriguing teaching tools such as those below.
http://www.joostrekveld.net/?p=803
In a previous post I’ve been discussing the beautiful materializations of the logical notation by Shea Zellweger. I was very much surprised to see him discussed by Louis Kauffman at the end of his book pdf about ‘Laws of Form’ which I mentioned in the previous post. Kauffman even made a version of Zellweger’s ‘logical garnet’ based on Spencer-Brown’s symbols !
A Version of the Logical Garnet Suited to Laws of Form
~