A conventional mathematical approach to describe how boundary forms work would be to first construct a Domain of all possible patterns of containment, the language of boundary forms. The James rules convert members of the pattern language into other valid members of the pattern language. Closure restricts the transformations themselves from generating or accepting forms that are not in the language.
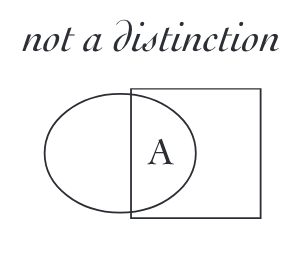
([A)] is not a valid containment pattern
For example ([A)] is not a valid containment pattern: We are considering here only the act of Distinction. A boundary identifies a difference. Set Intersection denies that difference.
Fortunately the pattern language of containment has physical realizations that clearly identify valid containment patterns.
The above invalid pattern would require us to **place a physical A in two different containers at the same Time**. Or it might require us to be able to **construct physical containers that intersect one other**, an impossible construction if we wish to maintain the integrity of physical boundaries. [ ⇒ Bisociation ⇒ Juxtaposition of Two Concepts ⇒ Poetic Pages]
The form ([A)] is possible as an imaginary pattern, but that extension to the concept of containment would also require a completely new mapping to the interpretation. That type of mapping is even difficult to write in conventional notation. Function notation also obeys the structural restrictions of containers. But we could read ([A)] as a Venn diagram, for instance, where the round- and square- boundaries each identify a set, and A identifies the intersection of both sets. The two overlapping functions become two different properties shared by the single object A.
Alternatively, we might introduce the logical concept AND to be able to say that A is contained both by ( ) and by [ ]. From the perspective of containment, the concepts of overlap, intersection and logical conjunction are necessarily imaginary concepts, in the meta-language or possibly imported from a different mathematical system.
~
BRICKEN, William, 2019. Iconic Arithmetic Volume I: The Design of Mathematics for Human Understanding. Unary press. ISBN 978-1-73248-513-6, p. 216–218.